uvod
Razstavljanje izrazov / A kifejezések szorzattá alakítása
Uvod / Bevezető
V prejšnjem
poglavju smo se učili razčlenjevati izraze, v tem poglavju pa se bomo učili
razstavljati izraze. Postopka sta si nasprotna. / Az előző
fejezetben a kifejezések szorzásáról tanultunk, ebben pedig a kifejezések szorzattá alakításáról tanulunk. A két eljárás egymás fordítottja.

Naslednji zgled prikazuje razliko med razčlenjevanjem in razstavljanjem algebrskega izraza. / Az alábbi példa az algebrai kifejezés szorzása, valamint szorzattá alakítása közötti különbséget szemlélteti.
Zgled / Példa
razstavljanje / felbontás
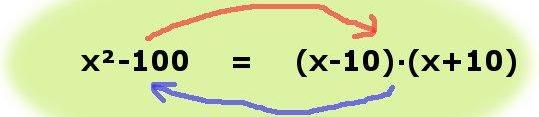
razčlenjevanje / szorzás
Razstaviti oziroma razcepiti izraz pomeni, izraz zapisati kot produkt več faktorjev (izrazov), zato postopek imenujemo tudi faktorizacija. V nadaljevanju bomo spoznali nekaj obrazcev, ki jih uporabljamo pri razstavljanju dvočlenikov in tričlenikov. Z razstavljanjem izrazov, ki imajo več kot tri člene, se na tem mestu ne bomo ukvarjali. Vedeti je treba tudi to, da v množici realnih števil nekatere izraze lahko razstavimo, drugih pa ne.
A kifejezés szorzattá alakítása a kifejezés több tényező szorzataként való felírását jelenti, ezért az eljárást a kifejezések tényezőkre bontásának is nevezzük. A folytatásban meg fogunk ismerni néhány képletet, amelyeket a kéttagú és háromtagú kifejezések szorzattá alakításakor alkalmazunk. A több mint három tagot tartalmazó kifejezések felbontását ezen a helyen nem tárgyaljuk. Tudnunk kell azt is, hogy a valós számok halmazában némely kifejezést tényezőkre lehet bontani, némelyt viszont nem.
Kateri izrazi so razstavljeni? / Mely kifejezéseket írtuk fel több tényező szorzataként?
|
$(x+2)(x+3)(x+4)-1$
|
|
$4-x(x-5)$
|
|
$(x+10)-(x+10)$
|
|
$2x(x-2)(x+3)$
|
|
$-x(x^2+4)-x^2$
|
|
$x^2+4x+3$
|
|
$(2x-1)-(x+3)(x+4)$
|